★ お 遊 び の 数 学 ★
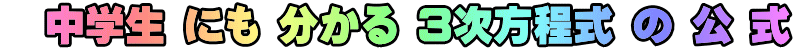np - 1 
http://www.newhp.kame3,org/newpage15.html
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
x 3 + a x 2 + b x + c = 0 
f ( x ) = 0 → x 1 x 2 x 3
1.jpg)
異なる３つ の 解 二 重 解 三 重 解
1.jpg)
２ 次方程式 の 解 は ４０００ 年 前 バビロニア で 発 見 されたと い う
３ 次方程式 の 解 は １６ 世 紀 イタリア 数学者 カルダノ ( フォンタナ )
カルダノ と フオンタナ の エピソード
カルダノ は フオンタナ に 懇 願 し て 三次方程式 の 解 の 公 式 の を
誰 に も 話 さ な い か ら と 言 つ て 聞 き 出 し ま し た
ところが カルダノ 自 分 の 数 学 の 著 書 に 載 せ て しまつた
従つて 世 の 数 学 者 は 三次方程式 の 解 の 発 見 は カルダノ と 知 る
Creｄit Yahoo
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
★ 前 書 き
★ ３ 次方程式 の 解 の公 式 の 導 出 の 展 開 式
★ 展 開 式 の 中 で 分かり にくい と こ ろ 行 間 説 明 を 加 えました
展 開 式 と 対 比 し て 見 る と 参 考 に なるか と 思 います
★ お 遊 び の 数 学 Welcom to My Homepage http://www.newhp.kame3.org/
★ 後 書 き
★ 参 考 資 料 三 次 方 程 式 の判 別 式 の 意 味 と 使 い 方 カルダノ の 公 式
●★★
★★●★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
★ 前 書 き
私 ご と で 恐 縮 ですが 。会社 を 定 年 退 職 してから 認 知 症 予 防 のためと 思いまして
お 遊 び の 数 学 で 暇 つ ぶ し を しようと 思 い ました
私 は 小学生 子供 の 頃より、算 数 、数 学 が 好 き でした
卒業後 、クラス会で温泉一拍旅行 があつた時、女の子 から 三 輪 さん は 数 学 の 天 才 だつたよね
と 冗 談 を 言 われ ました
私 が 数 学 だけ 、よく できた こと を 種 あ か し します と
私 は 、貧 乏 百 姓 の ６ 人 兄 弟 の 次 男
今の子供のよう に 、小 使 い を もらつて マンガ , 雑 誌 を 買える 環 境 ではありませんでした
兄 が 勉 強 ずきで 、学 校 から 帰つて くると よ く 勉 強 して おりました
私 は その 周 り で 、ちょろ ～ 遊んで いると よく 数 学 の 問 題 を 教えて くれました
そして 、この 問 題 は 解 けるか といつて 応 用 問 題 を 出 して く れました
私 は 、すら ～ と 答 え が 出 せ た よ う で す 兄 の 教 え 方 が う ま かつた た め でしょう
小 学 校 、新 学 期 なる と 教 科 書 が く ば ら れます
私 は 、数 学 の 教 科 書 だ け は 殆 ど 勉 強 する 必 要 は ありませんでした
兄 に 教 え ら れ た た め 一 年 先 を 走 つ て お り ま し た
時 間 年 月 の 位 相 が ず れ て い た だ け で す
女 の 子 の い う 天 才 で は あ り ま せ ん
ところで、私 が ３ 次 方程式 の 解 の 公 式 に 出 会 つた の は ７５ 才 の 頃 今 か ら １０ 年 以 上 前 です
パソコン で Yahoo Google Youtube 等 で インターネト サーフィス ( 資 料 検 索 )
数 学 の 関 数 、方 程 式 等 について 資 料 を 拾 い 集 め て 勉 強 し て おりました
その 中 で 関 連 資 料 と し て ３ 次 方 程 式 の 解 の 公 式 が 目 に とまり ました
３ 次 方 程 式 の 解 の 公 式 の 導 出 方 法 は 何 通 り か あ り ま す
● カ ル ダ ノ の 方 法 ( 実 は フォンタナ )
Crdit Yahoo
● ピ エ ト の 解 三 角 関 数 の ３ 倍 角 の 公 式 を 応 用 し た も の
cos 3α = 4 cos3 α - 3 cos α
● ラグランジュ の 方 法
● 円 錐 曲 線 に よ る 作 図
私 は 、カ ル ダ ノ の 方 法 が 比 較 的 分 か り 安 そ う な の で これで 勉 強 し ま し た
実 は , 私 クローバ- ビ ラ ( 健 老 リハビリ センター ) に 入 所 中 で す
コ ロ ナ 騒 ぎ で 家 族 の 面 会 も 許 さ れ ま せ ん 何 に も 、す る こ と が な い の で
3 次方程式 の 解 の公 式 の 導 出 の 展 開 式
について、中学生 にも 分かる ように やさしく 、説 明 し た 小 冊 子 を 書 い て み る こ と に しました
3 次方程式 の 公 式 は 高 校 の 数 学 教 科 書 に 載 つ て い な い の で
勉 強 し た こ と が あ る 方 は 殆 ど な い と 思 い ま す
展 開 式 の 内 容 は 数 学 と いう よ り マジシャン の マジツク の
たね あ か し を している よ う に 思 え ま す
挑 戦 し て み て く だ さ い
¨ ★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
★ 3 次方程式 の 解 の 公 式 の 導 出 の 展 開 式
、
x 3 + a x 2 + b x + c = 0 解 x 1 x 2 x 3
展 開 式 は 行 間 説 明 な し に 。羅 列 し ま し た
どうして そのように 展 開 するのか 、展 開 できるのか 、理 解 、納 得 できない ところが
あるかと、思いますが 、先ずは 、最 後 まで 読み 下して ください。
繰 り 返 し 、挑 戦 していると 、そうか 、そういう ことか 、と 気 ず く ことが 、あります
私 は 、全 貌 を 理 解 、納 得 するのに 、３ ケ 月 くらい、かかりました
気 長 に 、３ ケ 月 も、挑 戦 し続ずけた ので 、A ４ ４ ～ ５ 頁 ある 展 開 式 を 、
頭 から しつぽ まで 丸 暗 記 できて おりました
以 下 カルダノ ( 実 は フォンタナ ) の ３ 次 方 程 式 の 解 の 公 式 の 展 開 式
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ S - 1 の S は Section ( 節 ) の 頭文字
◆ S - 1 x = y - ( 1/3 ) ・ a と 変 数 変 換 する
二 項 定 理 参 照 ( a + b ) 2 = a 2 + 2a b + b2 )
( a + b ) 3 = a 3 +3 a2 b +3 a b 2 +b3 )
x 3 + a x 2 + b x + c = 0
( ( y - ( 1 / 3 ) a ) 3 + a ( ( y - ( 1 / 3 ) a ) 2 + b ( y - (1 / 3 ) a ) + c = 0
( y 3 - a .y 2 + ( 1 / 3 ) a 2 . y - ( 1 / 27 ) a 3 )
+ ( ( a . y 2 - ( 2 / 3 ) a 2 .y + ( 1 / 9 ) a 3 )
+ ( b y - ( 1 / 3 ) a b )
+ c = 0
y 3 + ( b - ( 1 / 3 ) a 2 ) y + ( ( 2 / 27 ) a 3 - ( 1 / 3 ) a b + c ) = 0
y 3 + 3 p y + 2 q = 0
3 p = b - (1 / 3 ) a 2 p = ( 1 / 3 ) b - '( 1/ 9 ) a 2
2 q = (2 / 27 ) a 3 - ( 1 / 3 ) a b + c q = ( 1 / 27 ) a 3 - ( 1 / 6 ) a b + ( 1/2 ) c
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ S - ２
y 3 + 3 p y + 2 q = 0
( u + v ) 3 + 3 p ( u + v ) + 2 q = 0
( u 3 + 3 u 2 v + 3 u v 2 + v 3 ) + 3 p ( u + v ) + 2 q = 0
｛ こ の 行 間 は 展 開 式 が か な り スキップ し て い ま す ｝
( u 3 + v 3 + 2 q ) + ( u 3 v 3 + p 3 ) = 0
↓ ↓
こ こ も スキップ しています
( u 3 + v 3 + 2 q ) = 0 u 3 + v 3 = - 2 q
連 立 方程式
( u 3 v 3 + p 3 ) = 0 u 3 . v 3 = - p3
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ S - 3 u 3 と v 3 を 解 とする ２ 次 方 程 式
z 2 - 2 q z - p 3 = 0
z の ２ 次方程式 の 解 z 1 = q + √( q 2 + p 3 )
z 2 = q - √( q 2 + p 3 )
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ S - 4 ここから 、 変 数 変 換 を 逆 戻 り して 、
求 め る ３ 次 方 程 式 の 解 に
解 x 1 x 2 x 3 に たどり 着 く
u 3 = z 1 u 3 - z 1 = 0
v 3 = z 2 v 3 - z 2 = 0
立 方 完 成 の 式 ( 一 次 方 程 式 ) 3 = ( 常 数 ) 3
3 √ ( 一 次 方 程 式 ) 3 = 3 √ ( 常 数 ) 3
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ S - 5 u 3 と v 3 の ３ 次 方程式 の 解 を 求 め る
u 1 = 3√ｚ１ = 3√( q + √( q 2 + p 3 ) )
u 2 = ( ( - 1 + i √3 ) / 2 ) . 3√z 1
= ( ( - 1 + i √3 ) / 2 ) .3√( q + √( q 2 + p 3 ) )
u 3 = ( ( - 1 - i √3 ) / 2 ) . 3√z 1
= ( ( - 1 - i √3 ) / 2 ) .3√( q + √( q 2 + p 3 ) )
v 1 = 3√ｚ2 = 3√( q + 3√( q 2 + p 3 ) )
v 2 = ( ( - 1 + i √3) / 2 ) . 3√z 2
= ( ( - 1 + i √3) / 2 ) .3√( q + √( q 2 + p 3 ) )
v 3 = ( ( - 1 - i √3) / 2 ) . 3√z 2
= ( ( - 1 - i √3) / 2 ) .3√( q + √( q 2 + p 3 ) )
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ S - 6 y = u + v に 戻 る
u + v は 前 記 u1 ～ u3 v1 ～ v3 よ り
9 通 り の 組 み 合 わ せ が で き る.
i
u 1 + v 1 u 1 + v 2 u 1 + v 3
u 2 + v 1 . u 2 + v 2 u 2 + v 3
u 3 + v 1 ... u 3 + v 2 u 3 + v 3
この 9 通 り の 組み合わせ の 中 から y の ３ 次方程式 の 解 ３ 個 を 選 ぶ y 1 y 2 y 3
u + v と u . v は 連 立 方 程 式 で あ る
従 つ て 。 u + v で あ る と 同 時 に u . v = - p で な け れ ば な ら な い
u + v の ９ 通 り の 組 み 合 わ せ で u . v = - p が 成 立 す る の は
y 1 = u 1 + v 1 = - p
y 2 = u 2 + v 3 = - p
y 3 = u 3 + v 2 = - p
y 1 y 2 y 3 の ３ 個 が 選 べ ま し た
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ S - 7 最 後 に x = y - ( 1 / 3 ) . a の 変 数 変 換 に 逆 戻 り し て
３ 次 方 程 式 の 解 x 1 x 2 x 3 公 式 を 導 出 しま す
x1 = y 1 - ( 1 / 3 ) . a = ( u 1+ v 1 ) - ( 1 / 3 ) .a = ( 3√z 1 + 3√z 2 ) - ( 1 / 3 ) . a
= ( ( ( 3√( q + √( q 2 + p 3 ) ) + ( ( 3√( q - √( q 2 + p 3 ) ) - (1 / 3).a
= 3√ ( ( 4 / 27 ) a3 - ( 2 / 3) a b + 2 c ) ) + 3√( ( 4 / 27 ) a 3 - ( 2 / 3) a b + 2 c ) ) 2
+ ( ( 1 / 3 ) .b - ( 1 / 9 ) .a 2 ) ) 3
+ 3√ ( ( 4 / 27 ) a3 - ( 2 / 3) a b + 2 c ) ) - √( ( 4 / 27 ) a 3 - ( 2 / 3) a b + 2 c ) ) 2
+ ( ( 1 / 3 ) .b - ( 1 / 9 ) .a 2 ) ) 3
x2 = y 2- ( 1 / 3 ) . a = ( u 2 + v 3 ) - ( 1 / 3 ) .a
= ( ( - 1 + i √3 ) / 2 ) ). 3√z 1 + ( ( - 1 - i √3 ) / 2 ).) 3√z 2 - ( 1 / 3 ,a )
= ( ( - 1 + i √3 ) / 2 ) ) ( ( 3√( q + √( q 2 + p 3 ) ) + ( ( - 1 - i √3 ) / 2 ) ( 3√( q - √( q 2 + p 3 )
- ( 1 / 3 ,a )
= ( ( - 1 + i √3 ) / 2 ) ) ( ( 3√( q + √( q 2 + p 3 ) )
+ ( ( - 1 - i √3 ) / 2 ) ( 3√( q - √( q 2 + p 3 ) - ( 1 / 3 ,a )
ｘ３ = y 3- ( 1 / 3 ) . a = ( u 3 + v 2) - ( 1 / 3 ) .a
= ( ( - 1 + i √3 ) / 2 ) ). 3√z 1 + ( ( - 1 - i √3 ) / 2 ).) 3√z 2 - ( 1 / 3 ,a )
３ 次 方 程 式 の 解 x 1 x 2 x 3 公 式 を 導 出 完 了
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
★ 展 開 式 の 中 で 分かり にくい と こ ろ 行 間 説 明 を 加 えました
展 開 式 と 対 比 し て 見 る と 参 考 に なるか と 思 います
私 は 、 こ の ３ 次 方程式解 の 公 式 の 導 出 をする 展 開 式 を 初めて 読 ん だ とき、
演 算 的 に 、機 械 的 に 追 い かける ことは 、 できた のですが,、
変 数 変 換 を 繰 り 返 し たり 、３ 次 方程式 を ２ 次 方程式 に 化 け さ せ たり 、すると 等
沢 山 、理 解 、納 得 できない ところが ありました 欲 求 不 満 に なりました
３ケ月ほど、根 気 よ く 挑 戦 していたら 、全 貌 が ほ ぼ 、理 解 、納 得 できました
私 が 、苦 労 し た ところ を 行 間 説 明 と し て 加 え ま し た の で
前 記 3 次方程式 の 解 の公 式 の 導 出 の 展 開 式 と
対 比 し て 参 考 に し て く だ さ い
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ D = 01 の D は Dificalt ( 難 し い 難 解 ) の 頭 文 字
◆ D = 01 x = y - (1 / 3 ) a と 変 数 変 換 す る こ と つずいて
y = u + v と 変 数 変 換 す る こ と
３ 次 方程式 の 解 の 公 式 を 導 出 する 展 開 式 に 、のめり 込んで ３ ケ 月 ほ ど 挑 戦 しつずけたら。
ほ ぼ 、全 貌 が つ か め ま し た
し か し 何 故 、x = y - (1 / 3 ) a と y = u + v
２ 段 が ま え に 変 数 変 換 す る か は 理 解 で き ず に 残 つ て 。 し ま い ま し た
７５ 才 で ３ 次 方程式 の 解 の 公 式 挑 戦 して から １０ 年 以 上 追 い か け 続 け て き ま し た
今、８８ 才 米 寿 で す
３ 次 方程式 の 解 の 公 式 の 発 見 者 カルダノ ( 実 は フォンタナ ) の 気 持 ち に な つ て、
何 故 、 x = y - ( 1 / 3) a y = u + v と 変 数 変 換 したのか 、憶 測 、推 測 してみました
な ん と 、憶 測 推 測 に 成 功 しました 飛 び 上 が る ような 喜 び を 感 じ ま し た
以 下 、 詳 し く 説 明 し ま す
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ D = 02 x = y - (1 / 3 ) a と 変 数 変 換 す る 理 由
３ 次方程式 は ２ 次方程式 の 延 長 上 に あるので 、３ 次方程式 の 解 の 公 式 が 参 考 になると思い、
2 次方程式 の 復 習 を しました
a x 2 + b x + c = 0
( x + ( b / 2 a ) ) 2 - ( b 2 / 4 a 2 ) + c / a = 0
( x + ( b / 2 a ) ) 2 = ( ( b 2 / 4 a 2) - ( c / a ) ) 平 方 完 成 の 式
( 一 次 方 程 式 ) 2 = ( 定 数 ) 平 方 完 成 の 式
x = ( b / 2 a ) ±√ ( ( b 2 / 4 a 2 ) - c / a )
= ( - b ± √ ( b 2 = 4 a c ) ) / 2 a = α 、β
解 と 係 数 の 関 係 α + β = - b / a α × β = c / a
このように 、2 次方程式 の 解 を求めるのに 平 方 完 成 の 式 ( 一 次 方 程 式 ) 2 = ( 定 数 ) に
２ 次方程式 の 式 を 変 形 しております
◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆
そ こ で 、 ３ 次方程式 の 発 見 者 フォンタナ ， カルダノ は
３ 次 方 程 式 x 3 + a x 2 + b x + c = 0 を
立 方 完 成 の 式 ( 一 次 方 程 式 ) 3 = ( 定 数 ) に
変 形 し て 、 この 両 辺 の 立方根 を 求めれば ３ 次方程式 の 解 x 1 x 2 x 3
の 一 つ x 1 は 求 め ら れ る と 考 え た と 憶 測 、推 測 し ま し た
し か し 、 x = y - (1 / 3 ) a と 変 数 変 換 した だけでは 立 方 完 成 の 式 に
変 形 で き ま せ ん
次 の y = u + v と 変 数 変 換 す る 必 要 が あ り ま す
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ D = 03 y = u + v の 変 数 変 換 の 展 開 式 に お い て
( u 3 + 3 u 2 v + 3 u v 2 + v 3 ) + 3 p ( u + v ) + 2 q = 0
( u 3 + v 3 + 2 q ) + ( u 3 v 3 + p 3 ) = 0
こ の 2 式 が 等 値 で あること の 説 明 ( 2021 12 ０６ 追 記 )
こ こ で も 数 学 記 号 等 式 〓 イコール が 便 利 に 使 わ れ て い ま す
( u 3 + v 3 + 2 q ) + ( 3 u 2 v + 3 u v 2 ) + 3 p ( u + v ) = 0
( u 3 + v 3 + 2 q ) + 3 u v ( u + v ) + 3 p ( u + v ) = 0
( u 3 + v 3 + 2 q ) + ( 3 ( u v + p ) + ( u + v ) ) = 0
こ の 等 式 は ( 0 ) + ( 0 ) = 0 で 成立する
す な わ ち ( u 3 + v 3 + 2 q ) = ０
3 ( ( u v + p ) + ( u + v ) ) = 0
( u v + p ) + ( u + v ) = 0
1 項 が ゼ ロ u v + p = 0 2 項 も ゼ ロ ( u + v ) = 0 = y で 成 立 す る が
2 項 も ゼ ロ で は ３次方程式 が なくなつて しまうので u v + p = 0 が 残 ろ
u v = - p 両 辺 を ３ 乗 して u 3 v 3 = - p3 と な る
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ D = 0４ y = u + v と 変 数 変 換 す る 理 由
= こ の 変 換 は u 3 、 v 3 の ３ 次 連 立 方程式 u 3 + v 3 = - 2 q
u 3 . v 3 = - p 3
を 作 り 更 に u 3 、 v 3 を 解 と す る2
３ 次 方 程 式 を 等 価 的 な ２ 次 方 程 式 に 化 け さ せ る
z 2 - 2 q z - p 3 = 0
こ の 、 z 2 次方程式 の 解 z 1 = q + √( q 2 + p 3 )
z 2 = q - √( q 2 + p 3 )
従 つ て 、 u 3 = z 1 v 3 = z 2 と
立 方 完 成 の 式 に 変 形 変 形 す る こ と が で き ま し た
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ D = 05 y = u + v の 変 数 変 換 の 展 開 式 に お い て
一つ の 、方 程 式 を 、二つ の 、方 程 式 に 分 解 す る こ と
( u 3 + v 3 + 2 q ) + ( u 3 v 3 + p 3 ) = 0
( u 3 + v 3 + 2 q ) = 0 u 3 + v 3 = - 2 q
連 立 方程式
( u 3 v 3 + p 3 ) = 0 u 3 . v 3 = - p 3
こ れ は 、 数 学 記 号 = 等 号 イコール の 果 た せ る 役 割 で す
左 辺 の 内 容 と 右 辺 の 内 容 が 等 し け れ ば = 等 号 イコール で 結 べ ま す
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ D 06 y = u + v の 変 数 変 換 の 展 開 式 に お い て
u 3 と v 3 の ３ 次 連立方程式 よ り u 3 と v 3 を 解 と す る
３ 次 方 程 式 を 等 価 的 な ２ 次 方 程 式 に 化 け さ せ る
u 3 + v 3 = - 2 q
連 立 方程式
u 3 . v 3 = - p 3
z 2 - 2 q z - p 3 = 0
こ の 、 ３ 次 方 程 式 から 等 価 的 な ２ 次 方 程 式 を 導 出 する なんて こ と
ど う し て も 理 解 納 得 できませんでした
しかたなく Yahoo インターネツト の 物 理 の カギシツ尾 の 掲示板 に問 い 合わせ しました
翌 日 メール で レスポンス あ り 回 答 を いただき ました
参 考 ま で に 物 理 の カギ シツ尾 の 掲示板 と の や り ち り を 載 せ て おきます
な ん と 2 次 方 程 式 の 解 と 係 数 の 関 係 を ご 存 じ か と か わ さ れ ました
解 と 係 数 の 関 係 α + β = - b / a
α × β = c / a
α = u 3 β = v 3 と す れ ば
2 次 方 程 式 の 解 と 係 数 の 関 係 と 全 く 同 形 と な り ま す
大 き な 落 と し 穴 に 落 ち て お り ま し た
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ D = 07 y = u + v の 変 数 変 換 の 展 開 式 に お い て
u 3 = z 1 u 3 - z 1 = 0
v 3 = z 2 v 3 - z 2 = 0
u の ３ 次方程式 と v の ３ 次方程式 の 解 を 求 め る く だ り が 現 れ ま し た
ま だ 、３ 次方程式 の 公 式 を 勉 強 中 に ３ 次方程式 の 公 式 の 解 を求 め よ と 言 わ れ て も
困 つ た こ と に な り ま し た
と こ ろ が 、 幸 い な こ と に 簡 単 な ３ 次方程式 の 解 は
因 数 分 解 す る こ と に よ つ て 求 め る こ と が で き る
u 3 = z 1 u 3 - z 1 = 0
解 を u 1 . u 2 . u 3 と す る
解 の 一 つ u 1 は u 3 = z 1 の 両 辺 の 立 方 根 3√u 3 = 3√z 1 .で
求 め る ことが で き る 他 の 二つ u 2 . u 3 は 因 数 分 解 に よつて求 め る
分 か り 安 く するために 簡 単 な ３ 次方程式 の 例 を 揚 げ て お き ま す
例 ① x 3 = 1 x 3 - 1 = 0
② x 3 = a 3 x 3 - a 3 = 0
x
解 を x 1 x 2 x 3 と す る
① x 3 = 1 x 3 - 1 = 0
解 の 一つ x 1 は x 3 = 1 の 両 辺 の 立 方 根 3√x 3 = 3√ 1= 1 と
求 め ら れ ま し た
他 の 二 つ x 2 、 .x 3 は x 3 - 1 = 0 を 因 数 分 解 に よつて 求 め る
( x 3 - 1 ) / ( x - 1 ) = x 3 + x + 1 = 0
x 1 = 1
x 2 = ( - 1 + i √3 ) / 2
x 3 = ( - 1 - i √3 ) / 2
② x 3 = a 3 x 3 - a 3 = 0 も 同 様 に 求 め る こ と が で き ま す
x 1 = a
x 2 = ( ( - 1 + i √3 ) / 2 ) a
x 3 = ( ( - 1 - i √3 ) / 2 ) a
以 上 、 例 ① ② の 説 明 お わ り ま す
ここで u 3 = z 1 u 3 - z 1 = 0
v 3 = z 2 v 3 - z 2 = 0
② x 3 = a 3 x 3 - a 3 = 0 と 同 形 な の で
x の 代 わ り に u 、 v a の 代 わ り に 3√z1 、 3√z2 を
代 入 す れ ば よ い 以 上
展 開 式 の 中 で 分かり にくい と こ ろ 行 間 説 明 完 了
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
★ お 遊 び の 数 学 Welcom to My Homepage
お 遊 び の 数 学 を ３０ 年 も 続 け て い た ら ホーム ページ が 沢 山 た ま り ま し た
開 い て 一 瞥 し て み て く だ さ い
◆ お 遊 び の 数 学 タイトル 目 次
ピタゴラス の 定 理 フィポナツチ 数 列 黄 金 比 円 筒 に 接つする 円 錐 と 球 球 の 表 面 積 と 体 積
数 学 の 公 式 で 面 白 い 関 係 を 発 見 論 証 問 題 因 数 分 解 の 公 式 数 学 関 数 について
三 次 方 程 式 の 解 の 公 式 四次方程式 三次方程式 の お 勉 強 一次、二次、三次 方程式 の 解
特殊関数 ガンマ Γ 関 数 ベツセル 関 数 ベータ 関 数 信頼性 確率密度 関数 e x の 微 分
フェルマー の 最終定理 パスカル の 三角形 ( 二項定理 ) 自然対数 e の 計 算 暗 算 問題
ガ ウ ス ２１ 世紀 の 数 学 七 大 難 問 ギリシャ の 三 大 難 問 関 数 。級 数と グラフ 図 形
マツスウエル の 方程式 数 学 教 室 ( 小 中 高 一般 ) 整 数 問 題 の 勉 強 牛 乳 パツク の 秘 密
ガ ロ ア 理 論 直線上 の ２ 点 A B 間 の 長 さ お 遊 び 数 学 そ の ２ 数 学 最 つとも 美 し い 公 式
不可能 方程式 積 分 で 面 積 を 求 め る シュデインガー 方 程 式 ブール 代 数 A B C 予 想
中学生 にも 分 か る 3次方程式 の 解 の 公 式 ２０２１ 開 成 高 校 入 試 数 学
数学の公式 不思議 な 関 係
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
◆ い ろ ん な グ ラ フ を 書 い て 楽 し ん で お り ま す
ど ん な 計 算 を し た か 想 像 し て 見 て く だ さ い
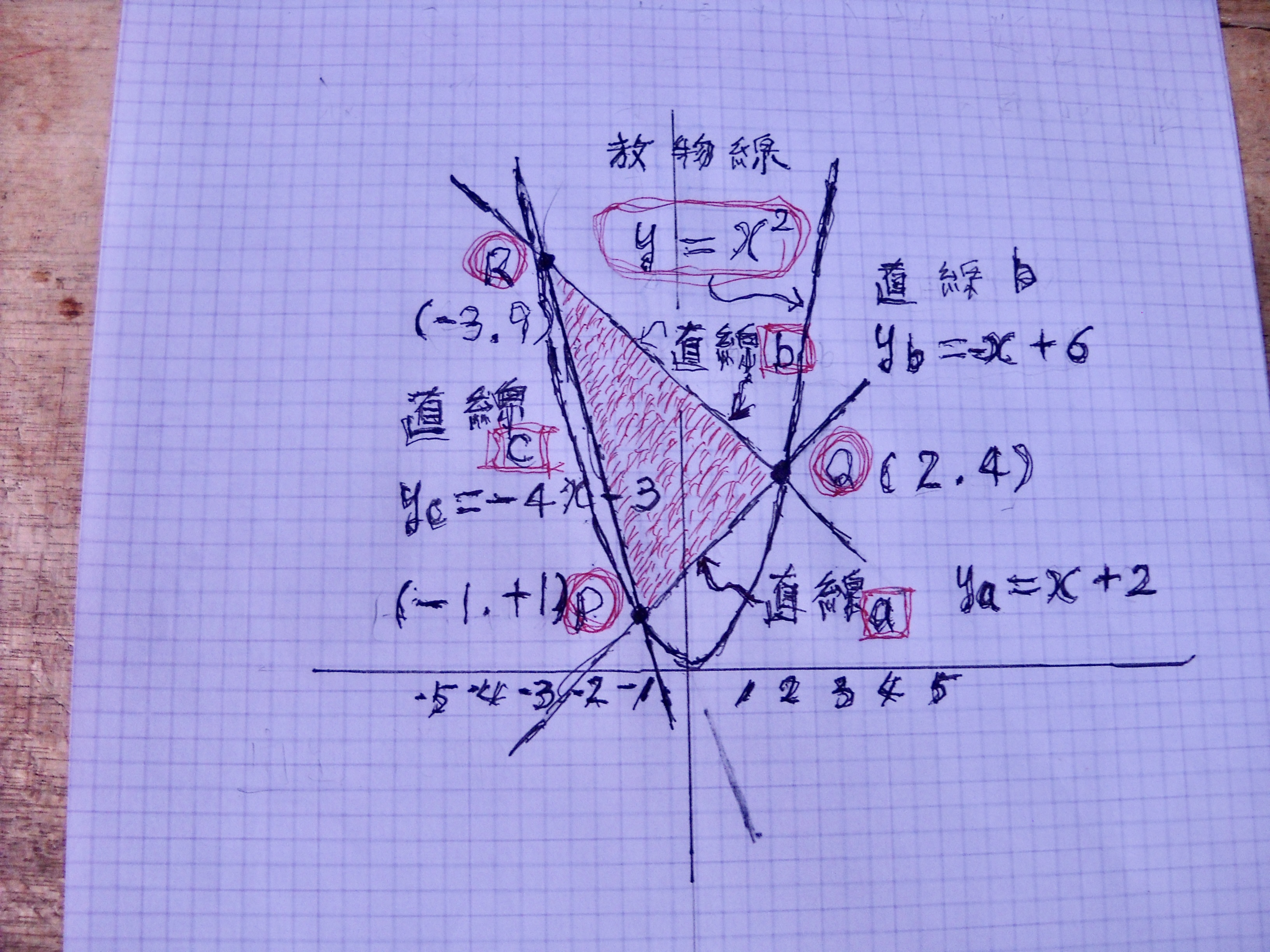
２０２１ 開 成 高 校 入 試 数 学
新 聞 を 見 た 時 は 解 け そ う も な い と 思 つ て い た こ の 問 題 が
何 日 か 後 夢 の 中 で 正 解 が 得 ら れ て お り ま し た 奇 蹟
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
【 夢 を 見 る と き 脳 は 】 読 売 新 聞 記 事 ２０２１ １１ １４
When Brains Dream 気つき もたらす 創 造 性
著 者 アントニオ ザドラ モントリオール 大 教 授 心 理 学
ロバート スチツクゴールド ハードバード 大 教 授 精 神 医 学
評 中 島 隆 博 東 京 大 教 授 哲 学 者
夢 に 興 味 を 持 つ て い た の で こ の 記 事 が 目 に 止 ま り ま し た
◆ 著 者 達 は 夢 を 【 睡 眠 に 依 存 す る 記 憶 処 理 一 形 式 】 だ と し て
【 NEXT UP 】 と い う モ デ ル を 提 案 し て い る
すなわち、可 能 性 理 解 のための ネットワーク 探 索 と いう もの
◆ 休息時 の 脳 は なにもしていないのではなく マインドワンダリング とりとめのない 思 考 状 態
にあり、活 発 に 動 いている のである
..... ◆ ドリーム ・ .インキュベーション
◆ イメージ・リハーサル 療 法
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
A B C 予 想
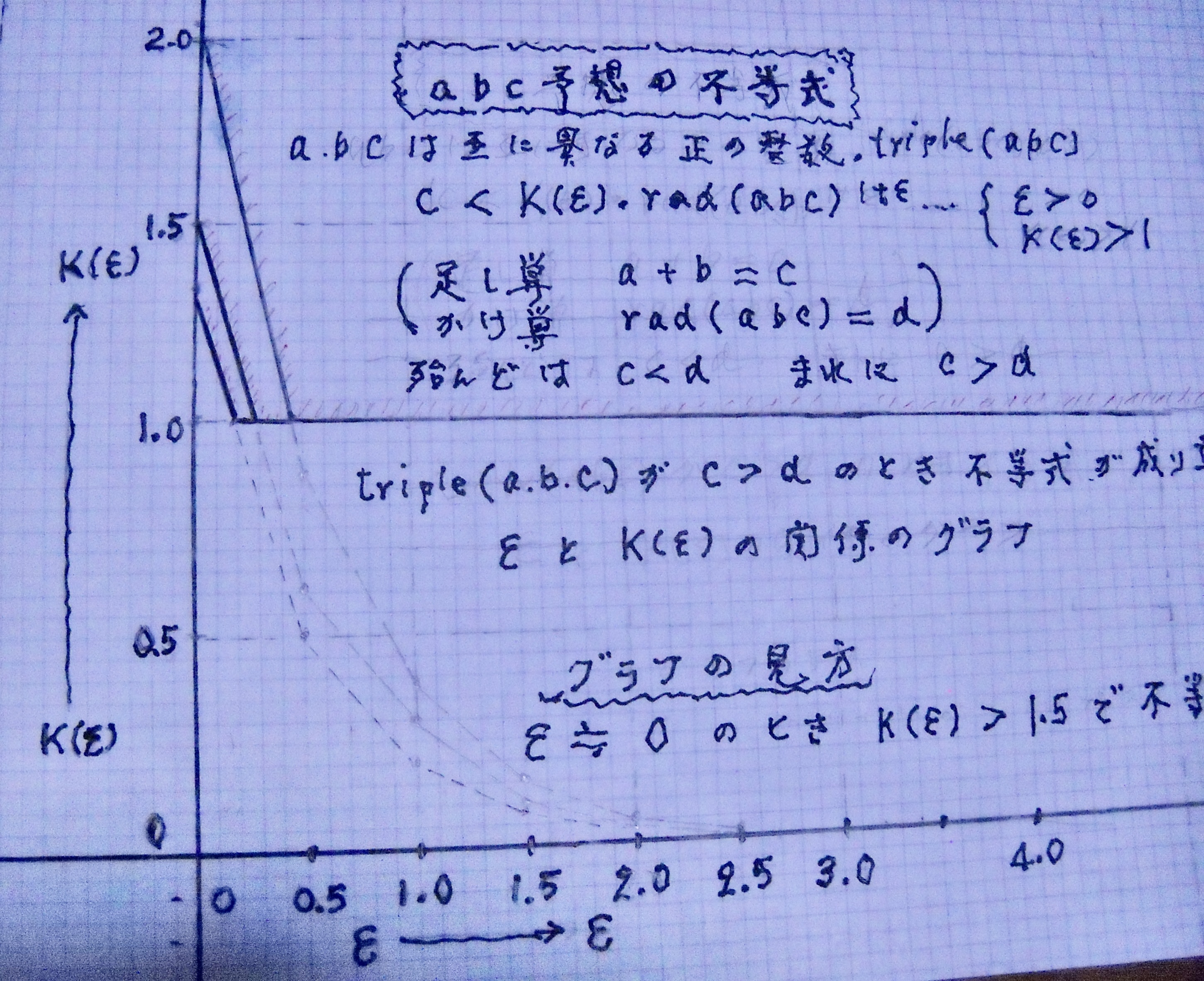
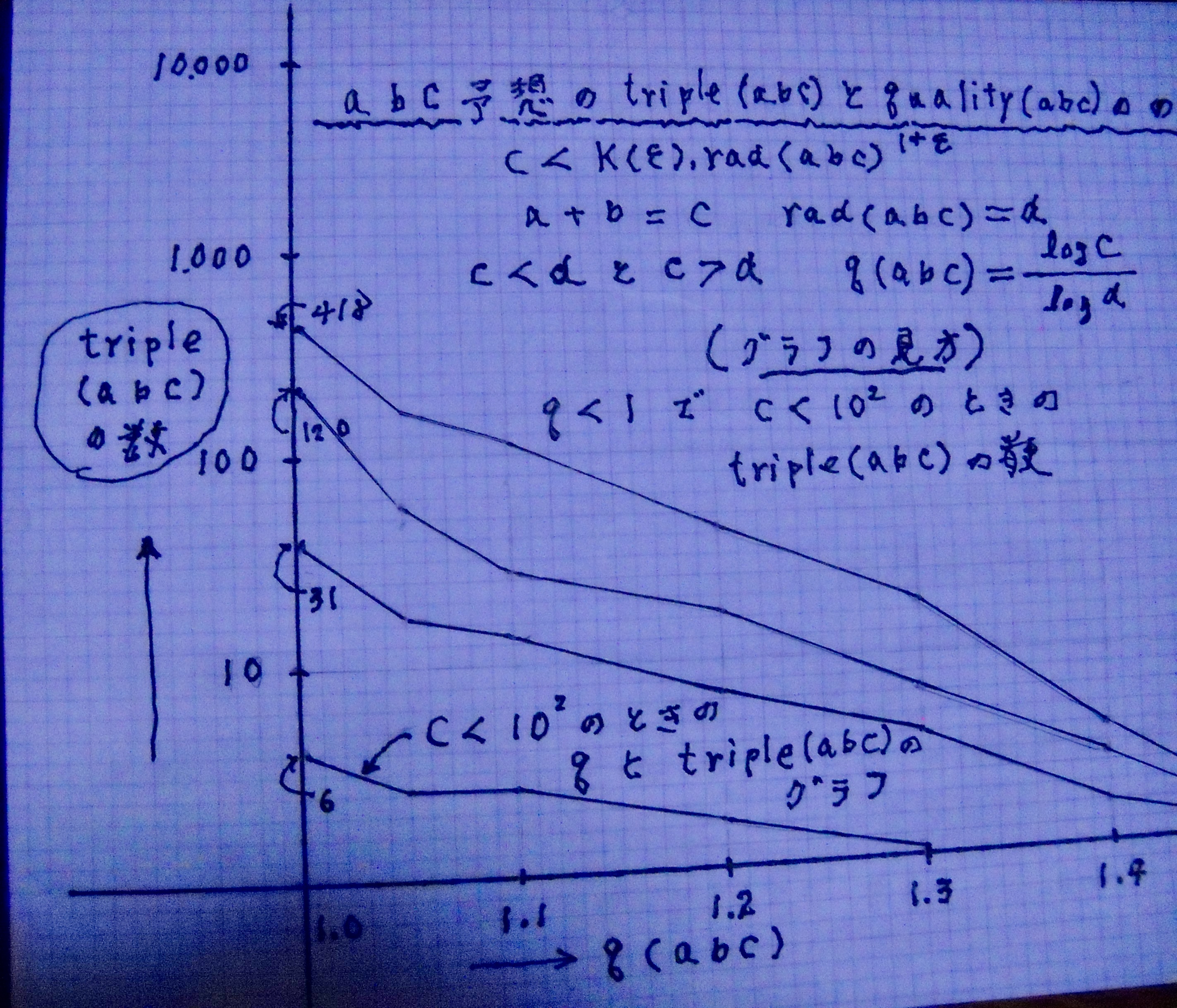
A B C 予 想 の 不 等 式 C ＜ K ・ d ( 1 + ε )
が C ＞ ｄ の 時でも 成立する ため の ε と K の 条 件 を 手 計 算 して
グラフ を 書 い て みました
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
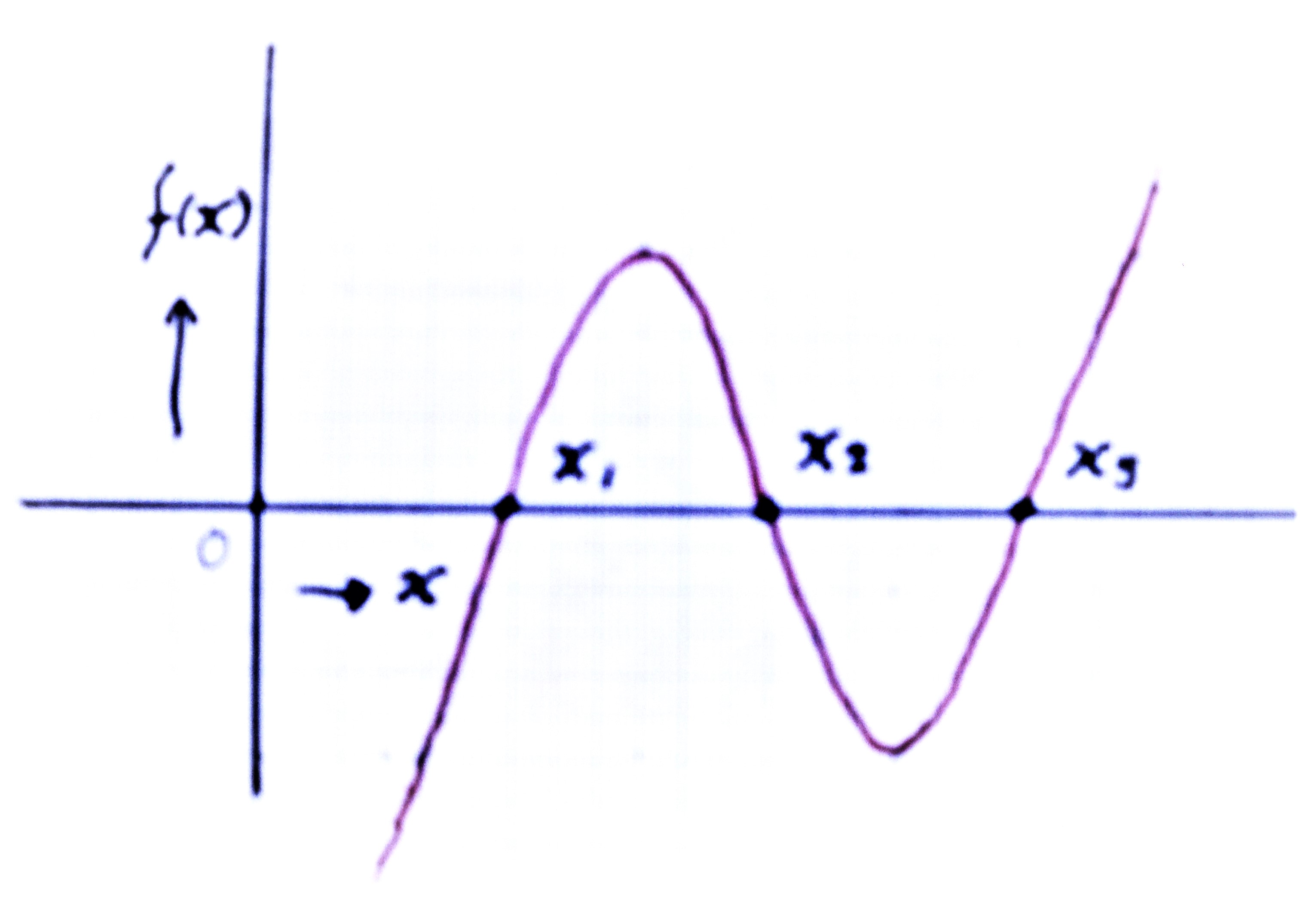
放 物 線 と 直 線
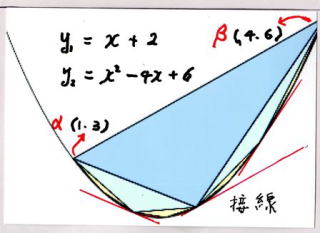
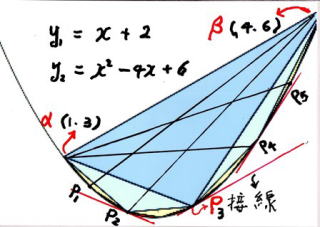
内 接 ３ 角 形
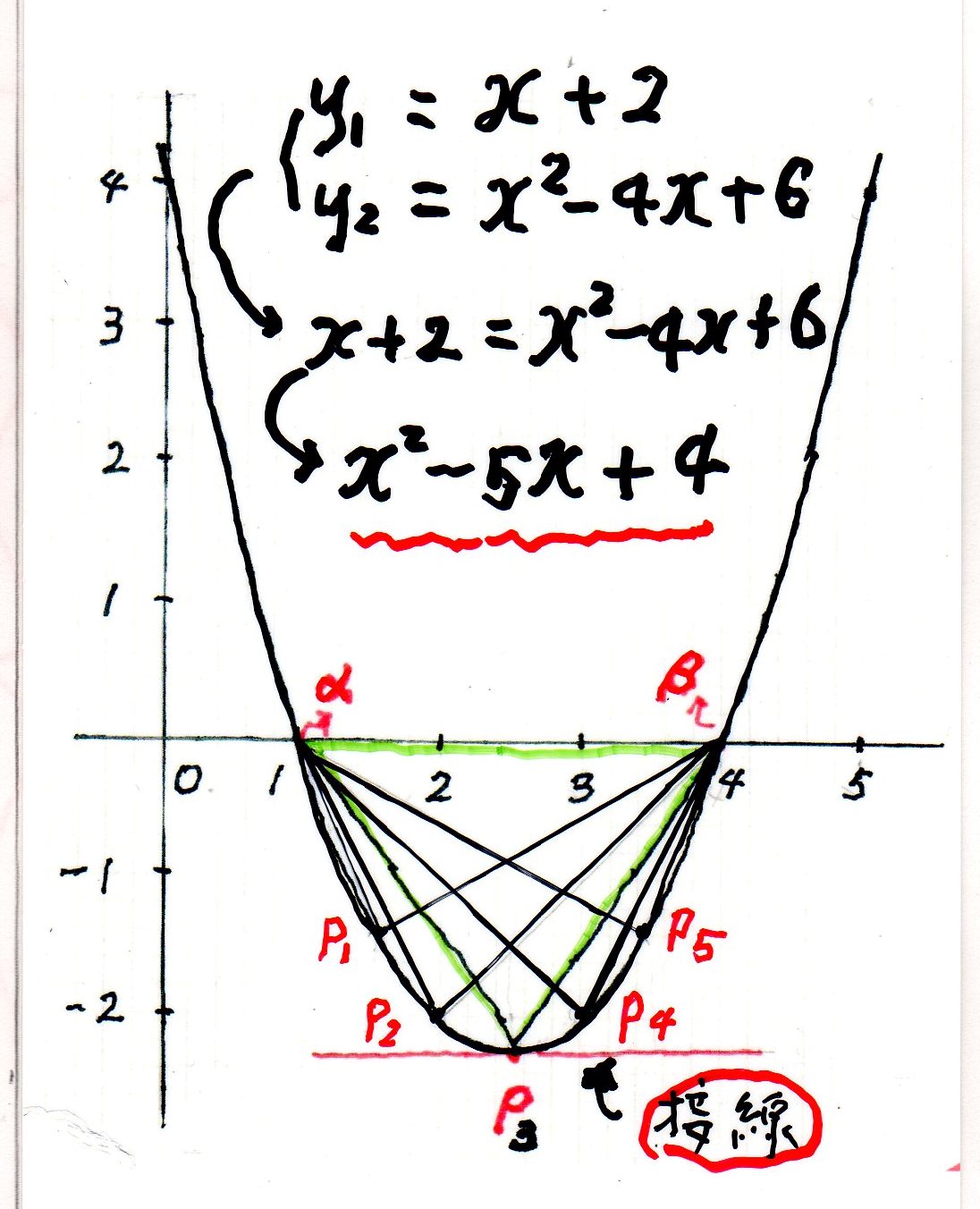
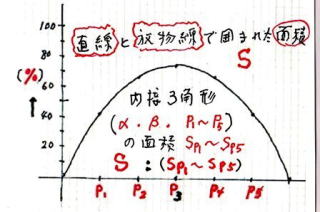
内 接 ３ 角 形 の 面 積
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
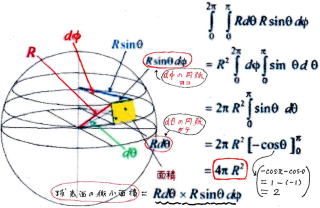
球 の 表 面 積 ２ 重 積 分 で 求 め る
初 め て ２ 重 積 分 を 体 験 し て み ま し た
★★★
★★★